

Command “eye” generates the identity matrix (try typing eye(3)). There are several MATLAB commands that generate special matrices.Ĭommand “rand” generates matrices with random entries (rand(3,4) creates a 3x4 matrix with random entries). Type:Ĭommand “det” computes determinants (we will learn more about determinants shortly).
#Augmented matrix how to#
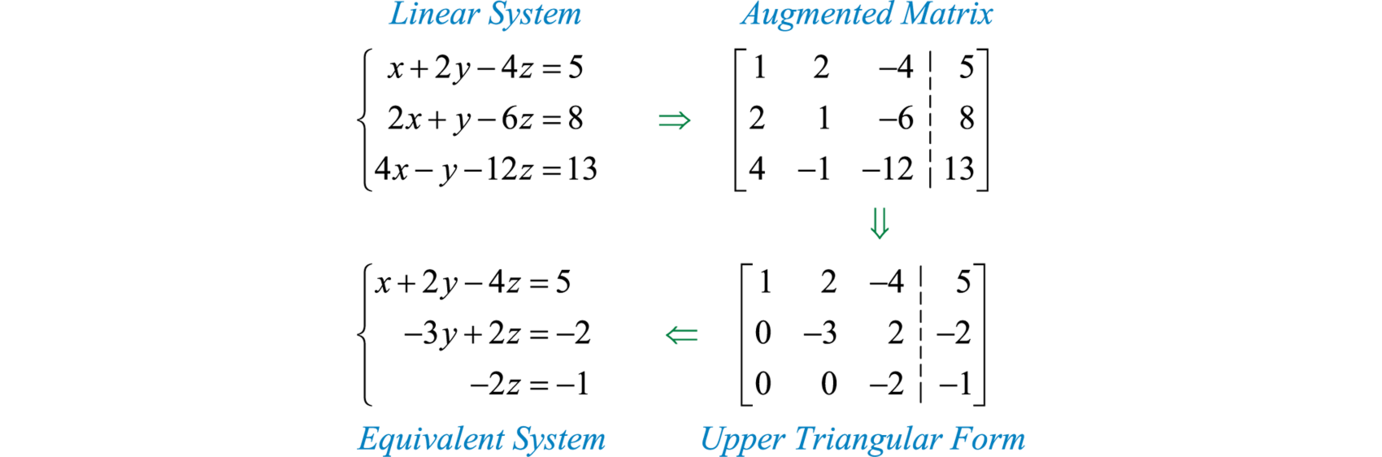
Typeįor more information on how to use the command.Ĭommand “inv” calculates the inverse of a matrix. To save your work, you can use command “diary”. You can also get help using command "doc". TypeĪnd you will get as a result a number of MATLAB commands that have to do with row echelon forms. Then you can row reduce to solve the system. Sometimes we do not know the exact command we should use for the problem we need to solve. Explanation: Create an augmented matrix by entering the coefficients into one matrix and appending a vector to that matrix with the constants that the equations are equal to. To find out more about command "help", typeĬommand "help" is useful when you know the exact command you want to use and you want to find out details on its usage. The algebraic method for solving the system of equations (finding the \(x\) and \(y\) values that satisfy both equations) is called row reduction. It is really just a matrix, but we call it augmented if we include information from both sides of the equation (the coefficients and the constants). For example, type:Īnd you will get information on the usage of "rref". This matrix is called an augmented matrix. It shows you how MATLAB commands should be used.

(Can we always use this method to solve linear systems in MATLAB? Experiment with different systems.)Ĭommand "help" is a command you should use frequently. This command will generate a vector x, which is the solution of the linear system. The symbol between matrix A and vector b is a “backslash”. You can also solve the same system in MATLAB using command You now need to use command “rref”, in order to reduce the augmented matrix to its reduced row echelon form and solve your system:Ĭan you identify the solution of the system after you calculated matrix C? You have now generated augmented matrix Aaug (you can call it a different name if you wish). In order to solve the system Ax=b using Gauss-Jordan elimination, you first need to generate the augmented matrix, consisting of the coefficient matrix A and the right hand side b: To generate a column vector b (make sure you include the prime ’ at the end of the command). This command generates a 3x3 matrix, which is displayed on your screen. The rank theorem in Section 2.9, which is the culmination of this chapter, tells us that the two questions are intimately related. The second question is perhaps a new concept for you. The first question is more like the questions you might be used to from your earlier courses in algebra you have a lot of practice solving equations like x 2 − 1 = 0 for x.
The resulting vector has the same number of entries as the number of rows of A, since each column of A has that number of entries. In order for Ax to make sense, the number of entries of x has to be the same as the number of columns of A : we are using the entries of x as the coefficients of the columns of A in a linear combination. Hints and Solutions to Selected Exercises.3 Linear Transformations and Matrix Algebra


 0 kommentar(er)
0 kommentar(er)
